Analise de Algoritmo: Uma introdução - Parte 1

Se você está iniciando no mundo da programação, é provável que tenha se perguntado: como medir a eficiência e o desempenho de um algoritmo, e como saber qual é o mais eficiente entre dois algoritmos que resolvem o mesmo problema?

Para responder a essas perguntas, é necessário entender que, ao ser executado por uma máquina, um algoritmo consome diversos recursos que podem ser medidos, como memória (complexidade de espaço), processamento (complexidade de tempo) e banda de internet, entre outros. Neste artigo, focaremos apenas na complexidade de tempo.

A complexidade de tempo é uma medida que descreve o tempo de execução de um algoritmo em relação ao tamanho da entrada. Ela representa a quantidade de tempo que um algoritmo leva para processar uma determinada quantidade de dados de entrada, ou seja, a complexidade está diretamente ligada à quantidade de dados que ele processa (N) e à quantidade de instruções executadas (Q).

Existem diferentes formas de medir a complexidade de um algoritmo:

Forma Empírica: Executa-se o algoritmo, mede-se o tempo de execução e compara-se entre diferentes algoritmos. No entanto, essa forma de medição pode ser influenciada por diversos fatores externos, como o hardware utilizado (desempenho do processador, memória RAM, etc.), a linguagem de programação e o compilador utilizados, além das entradas de teste e do ambiente de execução. Portanto, essa forma de medir a complexidade de um algoritmo pode não ser muito precisa e pode levar a conclusões equivocadas.
Forma Analítica: Um método mais preciso para medir a complexidade, que busca encontrar uma expressão matemática para traduzir o desempenho em quantidade de instruções. Diferentemente de calcular o tempo de execução em segundos ou minutos, o objetivo é contar as instruções que o algoritmo executa para chegar a uma fórmula matemática.

Em um computador real, podem ser encontrados vários tipos diferentes de instruções, como aritméticas (soma, subtração, multiplicação, divisão, resto, piso, teto), de movimentação de dados (carregar, armazenar, copiar) e de controle (desvio condicional, chamada e retorno de sub-rotinas). No entanto, é extremamente difícil medir o custo de cada instrução, já que eles podem variar entre hardwares, linguagens de programação e outros fatores físicos. Para fins didáticos, cada instrução é considerada de custo constante.

Exemplos

Vamos analisar dois algoritmos escritos em Python para ter um entendimento melhor.

Exemplo 1: Algoritmo que recebe dois números, faz a soma e retorna se é maior que cem ou menor:

number1 = int(input("digite um número: "))  # 2 instruções (leitura e conversão)
number2 = int(input("digite um número: "))  # 2 instruções (leitura e conversão)
soma = number1 + number2                   # 1 instrução (soma)

if soma > 100:                             # 1 instrução (comparação)
  print("maior que cem")                 # 1 instrução (impressão)
else:
  print("menor ou igual a cem")          # 1 instrução (impressão)

Na primeira e na segunda linha temos duas instruções: receber um valor e converter para inteiro;
Na terceira linha temos uma soma;
Na quarta temos uma comparação para checar se o número é maior que cem;
Na quinta e sétima linhas temos uma instrução em cada, mas como as estruturas if/else são mutuamente exclusivas, apenas uma delas será executada por vez.

Nesse caso, temos um custo constante de operações: T(n)=2+2+1+1+1=7T(n)=2+2+1+1+1=7 Demonstrando T(n)=c, ou seja, O*(1).

Exemplo 2: Algoritmo que percorre uma lista de números inteiros e analisa se é par ou ímpar:

def numeroPar(n):

  for i in n:                 # 1 instrução executada N vezes

      if i % 2 == 0:          # 2 instruções (resto + comparação) executadas N vezes

          print("Par")        # 1 instrução executada N vezes

      else:

          print("Ímpar")      # 1 instrução executada N vezes
          
#Nota: Essa contagem é uma simplificação didática para ilustrar que o número total de passos cresce proporcionalmente a N.

Na primeira linha do laço temos um for com uma instrução de atribuição que será executada N vezes (tamanho da lista).
Na linha seguinte temos duas instruções: calcular o resto da divisão e comparar se o resultado é igual a zero, cada uma executada NN vezes.
No corpo da condição temos uma instrução de impressão (print) executada a cada volta (N vezes).

Somando as instruções, temos a função: T(n)= n+n+n+n = 4n

Taxa de Crescimento

A partir de uma função que representa o custo, é possível realizar a análise gráfica do algoritmo e tentar prever a taxa de crescimento baseada no tamanho da entrada. Vamos utilizar a função T(n)=4n e entradas de tamanho 0, 10, 20, 30, 40 e 50:

T(0)=4×0=0
T(10)=4×10=40
T(20)=4×20=80
T(30)=4×30=120
T(40)=4×40=160
T(50)=4×50=200

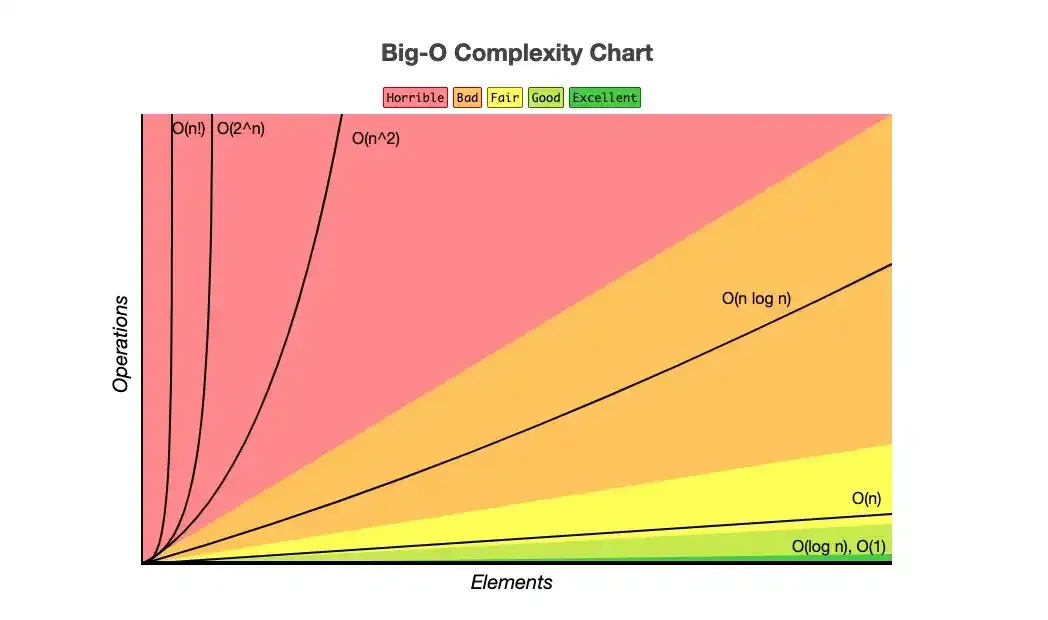
Classificação de Algoritmos (Notação Big-O)

Agora que você sabe calcular a complexidade de algoritmos, podemos classificá-los em algumas categorias principais:

1. Constante: O(1)

Algoritmos constantes são aqueles cuja complexidade não varia com o tamanho da entrada. Isso significa que, independentemente do volume de dados, o tempo de execução será sempre o mesmo.

Exemplo: Acessar um elemento de uma lista pelo índice ou imprimir uma mensagem fixa na tela.

2. Logarítmica: O(log⁡n)

O tempo de execução cresce de forma logarítmica em relação ao tamanho da entrada, ou seja, em uma taxa muito mais lenta do que o crescimento dos dados.

Exemplo: Pesquisa Binária. Uma lista ordenada é dividida pela metade sucessivamente até encontrar o elemento ou esgotar a busca.

3. Linear: O(n)

O tempo de execução é diretamente proporcional ao tamanho da entrada (N).

Exemplo: Busca linear ou percorrer e somar todos os elementos de uma lista.

4. Quadrática: O(n^2)

O tempo de execução cresce de forma proporcional ao quadrado da entrada (N^2). Esses algoritmos costumam ter desempenho ruim para entradas grandes.

Exemplo: Percorrer uma matriz N×N ou algoritmos com laços aninhados (loop dentro de loop).

5. Fatorial: O(n!)

Algoritmos fatoriais têm seu tempo de execução crescendo vertiginosamente com qualquer pequeno incremento na entrada. Algoritmos de complexidade O(n!) são aqueles que geram e testam todas as permutações possíveis de um conjunto de n elementos.

Exemplo clássico: Solução por força bruta para o Problema do Caixeiro-Viajante: dado um conjunto de cidades e as distâncias entre elas, encontrar a rota mais curta que visita todas as cidades exatamente uma vez e retorna à origem.
Para 4 cidades: 3!=63!=6 rotas
Para 10 cidades: 9!=362.8809!=362.880 rotas
Para 20 cidades: 19!≈1,21×101719!≈1,21×10^17 rotas (um supercomputador levaria anos)
Para 50 cidades: 49!≈6,08×106249!≈6,08×10^62 rotas (mais tempo que a idade do universo)

De maneira geral, algoritmos fatoriais tornam-se inviáveis para entradas médias e grandes, sendo necessário recorrer a algoritmos de aproximação, heurísticas ou programação dinâmica.

Conclusão

O propósito deste artigo foi apresentar uma introdução à análise de algoritmos, enfatizando a avaliação da eficiência em termos de complexidade de tempo. Compreender a análise de algoritmos é fundamental para se tornar um programador melhor, pois ajuda a implementar soluções mais eficientes e a prever o comportamento dos sistemas sob alta carga.

Sugestões de plataformas para praticar:

Agradeço a quem leu até aqui! Críticas, sugestões e correções são bem-vindas nos comentários abaixo ou no meu e-mail: nathansalesmello@gmail.com.

Próximo Artigo: Notação Assintótica: Melhor Caso, Caso Médio e Pior Caso (Em Breve).

Referências

Abrantes, Wagner. Análise da Complexidade de Algoritmos. Disponível em: https://www.iugu.com/iugu4devs/blog/analise-complexidade-algoritmos; Acesso em: 17 de abril de 2023.
Big-O Cheat Sheet. Disponível em: https://www.bigocheatsheet.com; Acesso em: 17 de abril de 2023.
Santiago, David. Análise de algoritmos: como se faz? Disponível em: https://algol.dev/analise-algoritmos-como-se-faz/; Acesso em: 17 de abril de 2023.
Cormen, T. H., Leiserson, C. E., Rivest, R. L., & Stein, C. Algoritmos: Teoria e Prática. 3ª edição. Elsevier, 2012.
imagem: https://www.bigocheatsheet.com/