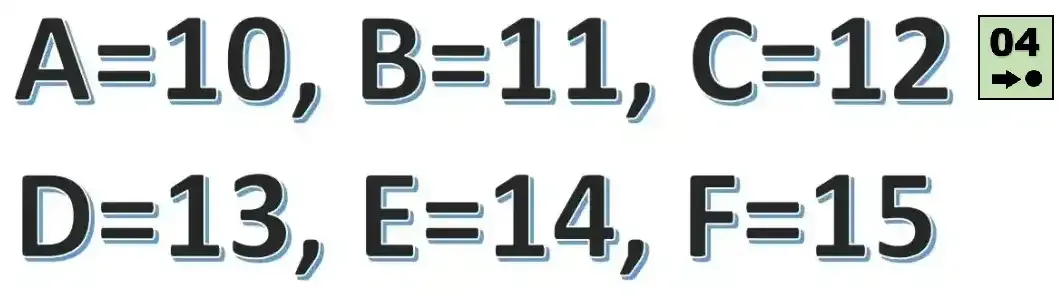<Direto ao Ponto 04> Números hexadecimais
<Direto ao Ponto 04> Números hexadecimais
Artigos da série: ( < ) Anterior | Índice | Seguinte ( > )
Olá, dev!
Este é mais um artigo da NOVA série DIRETO AO PONTO, que eu estou escrevendo para a DIO.
Ele vai apresentar uma introdução aos números hexadecimais, bastante usados em programação, e também uma introdução aos números octais.
Sumário
1. Introdução
2. Os números hexadecimais (base 16)
3. Os números octais (base 8)
4. Considerações finais
5. Referências
1 – Introdução
A NOVA série DIRETO AO PONTO enfoca artigos básicos sobre a programação e é voltada, principalmente, para os iniciantes.
Serão publicados artigos técnicos e artigos contando alguma história relacionada à computação/programação. Será publicado um artigo por semana, sempre no início da semana, pela manhã.
Neste artigo, eu vou apresentar os números hexadecimais, muito usados na área de informática, junto com os números binários, tratados no artigo anterior.
Os números octais, que também tem algum uso na informática, também serão apresentados.
Mais uma vez, quero deixar claro que boa parte do conteúdo escrito aqui vem da minha própria vivência pessoal ao longo dos anos em que convivi com a tecnologia e informática, desde 1980. Nestes casos, não haverá referências de livros, revistas ou sites, apenas as minhas lembranças pessoais.
2 – Os números hexadecimais (base 16)
Em programação, é comum usarmos o sistema de numeração hexadecimal, de base 16. Ele é muito usado nas aplicações seguintes:
· Definição de cores RGB, em CSS ou programas de imagens;
· Representação de instruções e dados em linguagem Assembly;
· Codificação de caracteres (código ASCII, UTF-8, etc.);
· Simplificação de números longos (bytes) em código binário;
Vamos fazer uma analogia para o sistema hexadecimal, repetindo tudo que foi mostrado até agora para o sistema binário.
São características desse sistema:
· Usa algarismos e letras para representar quantidades definidas;
· Usa 16 símbolos (de 0 a 9, e de A até F) para representar qualquer quantidade decimal;
· O zero é representado pelo algarismo 0;
· É um sistema posicional, ou seja, algarismos iguais podem valer quantidades diferentes dependendo da posição em que aparecem no número.
Como este sistema conta quantidades baseadas em conjuntos de 16 itens em cada ordem e só existem 10 algarismos (de 0 a 9), foram utilizadas algumas letras para representar as quantidades de 11 a 15:
A: representa 10 itens;
B: representa 11 itens;
C: representa 12 itens;
D: representa 13 itens;
E: representa 14 itens;
F: representa 15 itens;
A notação posicional divide o número em ordens. Cada ordem imediatamente superior representa um conjunto completo de itens da unidade inferior. Desta forma, podemos representar cada ordem usando os símbolos definidos para o sistema decimal (de 0 a F).
Quando uma ordem já tem o símbolo F, mais alto da sequência, e chega mais outro item, não existe outro algarismo para representar esta quantidade naquela ordem. Portanto, a quantidade de itens daquela ordem é zerada mais uma ordem imediatamente superior a ela é incrementada.
No sistema hexadecimal, não temos nomes para as ordens, como no decimal (e como eu fiz no binário, por simplificação didática). No entanto, a primeira ordem representa as quantidades de 0 a 15, a segunda ordem, imediatamente superior, representa os conjuntos de 16 itens, a terceira, conjuntos de 256 itens, e assim por diante.
Cada ordem representa 16 itens da ordem imediatamente inferior, ou seja, a 2ª ordem tem 16 unidades, a 3ª ordem tem 16 unidades da 1ª ordem (ou 256 unidades = 162, a 4ª ordem tem 16 unidades da 3ª ordem (ou 4096 unidades = 163, etc.
... | CONJUNTOS DE 256 UNIDADES | CONJ. DE 16 UNIDADES | UNIDADES
Em geral, em programação, só costumamos usar as duas primeiras ordens, agrupando os números em 2 dígitos decimais.
Veja os exemplos seguintes:
4 - Os números octais (base 8)
Este sistema é pouco usado, mas ele tem importância na representação da informação de permissões de manipulação de arquivos nos sistemas Unix e Linux.
Vamos fazer uma analogia para o sistema octal, repetindo tudo que foi mostrado até agora para o sistema hexadecimal.
São características desse sistema:
· Usa algarismos para representar quantidades definidas;
· Usa 8 símbolos (de 0 a 7) para representar qualquer quantidade;
· O zero é representado pelo algarismo 0;
· É um sistema posicional, ou seja, algarismos iguais podem valer quantidades diferentes dependendo da posição em que aparecem no número.
O uso que se faz deste sistema é mais para simplificação do que representar quantidades grandes usando a base 8. Ele é usado para simplificar números binários com 3 bits (de 000 até 111) em sequência, de 3 em 3 bits.
Por exemplo:
Número binário 000 representa a quantidade 0 em decimal, e 0 em octal também.
Número binário 001 representa a quantidade 1 em decimal, e 1 em octal também.
E assim por diante, até o binário 111, que representa 7 em decimal e 7 em octal também.
O número binário 000111011 pode ser separado em grupos de 3 bits, da direita para a esquerda. Caso o último grupo à esquerda não tenha 3 bits, deve-se completar os 3 bits com valores 0, que não alteram o valor do número
000 111 011
Representando cada conjunto de 3 bits pelo seu código octal correspondente, teremos 0 7 1.
Assim, o binário 000111011 pode ser representado pelo número octal 071.
Se você não está lembrado onde usou esta representação, veja a seguir.
Permissão para acesso a arquivos e diretórios do Linux (e Unix):
Deve ser configurada uma permissão para o dono (criador) do arquivo, o grupo a que ele pertence e para outros usuários;
Para cada um destes personagens, deve-se atribuir permissão de leitura, escrita e execução, da seguinte forma:
· r – permissão de leitura do arquivo (ou listagem do diretório);
· w - permissão de escrita no arquivo (ou criação de arquivos e diretórios dentro de um diretório);
· x - permissão de execução de um arquivo (executável) (ou acesso a um diretório pelo comando “cd”);
As permissões de acesso a um arquivo/diretório podem ser visualizadas com o uso do comando ls -la.
As letras (rwx) são agrupadas da seguinte forma:
-rwxr-xr-- fernando users ordena_texto
Separando as letras de 3 em 3, depois do primeiro símbolo, temos:
- rwx r-x r—
Onde:
- : se este primeiro símbolo for d, será um diretório, se for – será um arquivo;
rwx : permissão de leitura, escrita e execução do arquivo para o dono
r-x : permissão de leitura e execução do arquivo para o grupo, mas não de execução;
r-- : permissão apenas de leitura, para outros usuários, mas não de escrita nem de execução
Outra forma de representar estas permissões é indicando a habilitação (bit 1) ou desabilitação (bit 0) de cada permissão por meio de bits 0 e 1.
Desta forma, a permissão do exemplo ficaria assim:
- 111 101 100
· 111 - permissão habilitada para leitura, escrita e execução do arquivo para o dono;
· 101 - permissão habilitada para leitura e execução do arquivo para o grupo, mas não de execução;
· 100 - permissão habilitada apenas para leitura, para outros usuários, mas não de escrita nem de execução.
Pronto! Agora voltamos ao sistema octal.
111 representa a quantidade 7 no sistema octal, 101 representa 5 e 100 representa 4.
Portanto, as permissões para este arquivo seriam 754, cada número representando as habilitações de escrita, leitura e gravação do dono (7), grupo (5) e outros (4).
Eu não me lembro de ter usado o sistema octal para outra coisa em programação, além disso.
4 – Considerações finais
Este é mais um artigo da NOVA série DIRETO AO PONTO, que eu estou escrevendo para a DIO.
Neste artigo, foi apresentada uma introdução aos números hexadecimais, muito usados em programação, na parte de definição de cores, na codificação de caracteres ou em linguagem de Assembly.
Também foi dada uma introdução básica dos números octais, usados em alguns comandos do Linux.
Espero que tenha gostado. Até o próximo artigo, ainda nesta semana!
5 – Referências
Sem referências, tá tudo na minha cabeça (“in my head”).
“In your head, in your head
Zombie, zombie, zombie-ie-ie
What's in your head, in your head?
Zombie, zombie, zombie-ie-ie-ie, oh”
(Zombie – música do Cranberries) :-)
Mas, se você quiser uma bibliografia para se aprofundar no assunto, eu fiz uma pesquisa e, para o assunto deste artigo, gostei dessas:
[1] FERNANDES, Sthefania, Binário x decimal x Hexadecimal: Conheça os sistemas de numeração. Disponível em: <https://embarcados.com.br/binario-decimal-hexadecimal-sistemas-de-numeracao/>. Acessado em: 17/01/2024
[2] ROSA, Daniel, O comando LS do Linux – Como listar arquivos em um diretório e flags de opções. Disponível em: <https://www.freecodecamp.org/portuguese/news/o-comando-ls-do-linux-como-listar-arquivos-em-um-diretorio-e-flags-de-opcao/>. Acessado em: 17/01/2024
Artigos da série: ( < ) Anterior | Índice | Seguinte ( > )
