<Direto ao Ponto 02> O Sistema Decimal

Artigos da série: ( < ) Anterior | Índice | Seguinte ( > )

Olá, dev!

Este é mais um artigo da NOVA série DIRETO AO PONTO, que eu estou escrevendo para a DIO.

Ele vai focar em uma introdução aos sistemas numéricos, tratando do sistema decimal, como preparação para os próximos artigos, que tratarão dos sistemas binário e hexadecimal.

Sumário

1. Introdução

2. O sistema de numeração decimal

4. Considerações finais

3. Referências

1 – Introdução

A NOVA série DIRETO AO PONTO enfoca artigos básicos sobre a programação e é voltada, principalmente, para os iniciantes.

Serão publicados artigos técnicos e artigos contando alguma história relacionada à computação/programação. Será publicado um artigo por semana, sempre no início da semana, pela manhã.

Este artigo vai focar em uma introdução aos sistemas numéricos, tratando do sistema decimal, como preparação para os próximos artigos, que tratarão dos sistemas binário e hexadecimal, bem como da conversão entre bases de numeração.

Eu quero deixar claro que boa parte do conteúdo escrito aqui vem da minha própria vivência pessoal ao longo dos anos em que convivi com a tecnologia e informática, desde 1980. Nestes casos, não haverá referências de livros, revistas ou sites, apenas as minhas lembranças pessoais.

2 – O Sistema de Numeração Decimal

Desde o início da humanidade, sempre existiu a necessidade de realizar contagens. Era preciso contar as maçãs, ovelhas, filhos, soldados, estrelas, etc.

No início, eram usadas pedras para contar as ovelhas que iam pastar; as pedras eram recolhidas quando as ovelhas retornavam para saber se faltava alguma.

O problema é que cada povo descobria sua própria maneira de contar e representar as unidades. Os sistemas de contagem mais conhecidos são o egípcio, romano, sumério, maia, chinês e indo-arábico. O nosso sistema decimal deriva do sistema indo-arábico.

O antigo sistema romano tem algumas diferenças para o nosso sistema decimal e ainda hoje é usado em algumas atividades, como representação dos séculos, apêndices de um livro ou nos mostradores de alguns relógios.

Curiosidade: Você sabe como um mostrador de relógio representado por algarismos romanos identifica as 4 horas? Se você respondeu IV, está errado! Todas as horas usam algarismos romanos, mas 4 horas é representada por 4 tracinhos: IIII.

Sabia? Agora já sabe!!

Não acredita? Se você tem um relógio com algarismos romanos, dê uma olhada nele!!!

Arrá!!! Viu? Pois é! Agora pesquise para saber a causa. Eu pesquisei e já sei!

Ah, o seu não tem? Bem, alguns têm e outros não têm. Paciência! :-)

Sistema de Numeração Romano

São características desse sistema:

· Usa letras para representar quantidades fixas;

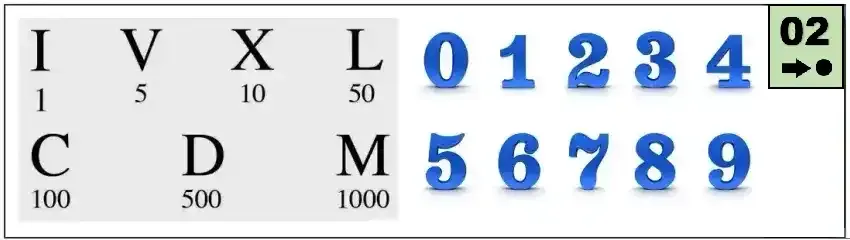
· Usa apenas 7 símbolos (I, V, X, L, C, D, M) símbolos para representar qualquer quantidade;

· Não existe forma de representar a quantidade zero.

· Não é um sistema posicional, ou seja, os símbolos valem a mesma quantidade em qualquer posição do número;

· Se um símbolo está à direita de outro símbolo que vale mais, seu valor será somará ao número;

· Para alguns símbolos se ele estiver à esquerda de um outro símbolo que vale mais o valor do símbolo menor será subtraído do número (exemplos: IV, IX, XL, CD. CM);

· Alguns algarismos (I, X, C, M) podem se repetir até 3 vezes seguidas (exemplos: II, III, XX, CCC, MM);

A seguir, são mostradas as quantidades representadas por cada algarismo romano:

I – 1,

V – 5,

X – 10,

L – 50,

C – 100,

D – 500,

M - 1000

Como exemplo, veja a quantidade representada por alguns números romanos:

Sistema de numeração decimal

São características desse sistema:

· Usa algarismos para representar quantidades definidas;

· Usa 10 símbolos (de 0 a 9) para representar qualquer quantidade;

· O zero é representado pelo algarismo 0;

· É um sistema posicional, ou seja, algarismos iguais podem valer quantidades diferentes dependendo da posição em que aparecem no número.

Exemplos:

133 = 100 + 30 + 3: o primeiro algarismo 3 representa 30 unidades enquanto o segundo 3 representa 3 unidades.

1001 = 1000 + 1: o primeiro algarismo 1 vale 1000; o segundo 1 vale 1 unidade.

Veja estes dois exemplos:

1234 = 1000 + 100 + 30 + 4

4321 = 4000 + 300 + 20 + 1

No primeiro exemplo, os algarismos 1234 (1, 2, 3 e 4) representam, na ordem (1234), a quantidade mil, duzentos e trinta e quatro itens. Já no segundo, veja que os mesmos algarismos 1234 (1, 2, 3, 4) representam, na ordem (4321), a quantidade quatro mil, trezentos e vinte e um.

É por isso que se diz notação posicional. Um mesmo algarismo pode representar diferentes quantidades de itens, dependendo da sua posição no número.

A notação posicional divide o número em ordens. Cada ordem imediatamente superior representa um conjunto completo de itens da unidade inferior. Desta forma, podemos representar cada ordem usando apenas os algarismos definidos para o sistema decimal (0 a 9).

Quando uma ordem já tem o algarismo 9, mais alto da sequência, e chega mais outro item, não existe outro algarismo para representar esta quantidade naquela ordem. Portanto, a quantidade de itens daquela ordem é zerada, mas a ordem imediatamente superior a ela é incrementada.

No sistema decimal, estas ordens são unidade, dezena, centena, milhar, etc. Uma dezena representa 10 unidades, uma centena representa 10 dezenas, um milhar representa 10 centenas, e assim por diante.

Cada ordem representa 10 itens da ordem imediatamente inferior, ou seja, 1 dezena tem 10 unidades, 1 centena tem 10 dezenas, 1 milhar tem 10 centenas, etc.

... | MILHARES | CENTENAS | DEZENAS | UNIDADES

Veja os exemplos seguintes:

| 1 | 2 | 3 | 4 |

Ele possui 1 Milhar, 2 Centenas, 3 Dezenas e 4 unidades

| 3 | 0 | 1 | 8 |

Ele possui 3 Milhares, 0 Centenas, 1 Dezena e 8 unidades

Agora vamos incrementar um número, por exemplo, 9:

| 0 | 0 | 0 | 9 |

Ele possui 0 milhares, 0 centenas, 0 dezena e 9 unidades, ou seja, ele representa 9 unidades.

Simplificando, só mostrando as ordens que vamos usar agora:

| DEZENAS | UNIDADES |

| 0 | 9 |

Se mais 1 item precisa ser adicionado à esta quantidade, não existe mais algarismo para representar quantidade acima do 9.

Então, a quantidade total de dez itens será representada por 1 dezena, sem nenhum item adicional na ordem das unidades, ficando assim:

| DEZENAS | UNIDADES |

| 1 | 0 |

Caso chegue mais 1 item (e sempre que chegar um novo item individual), ele será adicionado à ordem das unidades, que passará para 1.

| DEZENAS | UNIDADES |

| 1 | 1 |

E a quantidade total será 11 itens, com 1 dezena e 1 unidade

E como representar a retirada de 1 item da contagem? Bem, isso tem mais a ver com a parte de aritmética. (o tal empresta-1, diferente do vai-um daqui). Fica para outra vez!

Veja que 2345 =

2000 + 300 + 40 + 5 =

2 x 1000 + 3 x 100 + 4 x 10 + 5 x 1 =

2 x 10³+ 3 x 10² + 4 x 10¹ + 5 x 10⁰=

Resumindo, 2 milhares, 3 centenas, 4 dezenas e 1 unidade.

Ou seja, podemos decompor um número decimal em potências de 10, cada uma delas representando uma das ordens do número.

3 – Considerações finais

Este é mais um artigo da NOVA série DIRETO AO PONTO, que eu estou escrevendo para a DIO.

Neste artigo, foi apresentada uma introdução aos sistemas numéricos, focando no sistema decimal.

Essa foi uma preparação para os próximos artigos, que tratarão dos números binários, hexadecimais e da conversão entre bases numéricas.

Espero que tenha gostado. Até o próximo artigo, ainda nesta semana!

4 – Referências

Sem referências, tá tudo na minha cabeça (“in my head”).

“In your head, in your head

Zombie, zombie, zombie-ie-ie

What's in your head, in your head?

Zombie, zombie, zombie-ie-ie-ie, oh”

(Zombie – música do Cranberries) :-)

Mas, se você quiser uma bibliografia para se aprofundar no assunto, eu fiz uma pesquisa e, para o assunto deste artigo, gostei dessas:

[1] FERNANDES, Sthefania, Binário x decimal x Hexadecimal: Conheça os sistemas de numeração. Disponível em: <https://embarcados.com.br/binario-decimal-hexadecimal-sistemas-de-numeracao/>. Acessado em: 17/01/2024

Artigos da série: ( < ) Anterior | Índice | Seguinte ( > )