Tutorial básico: programado em um computado quântico

# Vamos ver como podemos implementar um circuito facilmente usando PennyLane.

# Importando PennyLane e NumPy

import pennylane as qml
from jax import numpy as np
import jax

##############################################################################

Criando um dispositivo:

Antes de podermos construir nosso nó quântico, precisamos inicializar um **dispositivo**.

Qualquer objeto computacional que possa aplicar operações quânticas e retornar um valor de medição

é chamado de **dispositivo** quântico.

Para este tutorial, estamos usando o modelo de qubit, então vamos inicializar o dispositivo ``'lightning.qubit'``

fornecido pelo PennyLane.

dev1 = qml.device("lightning.qubit", wires=1)

##############################################################################

Argumentos:

* ``name``: o nome do dispositivo a ser carregado

* ``wires``: o número de subsistemas para inicializar o dispositivo

Aqui, como só precisamos de um único qubit para este exemplo, definimos ``wires=1``.

##############################################################################

Construindo o QNode:

Agora que inicializamos nosso dispositivo, podemos começar a construir um**nó quântico** (ou QNode).

QNodes são uma abstração encapsulada de uma função quântica, descrita por um ircuito quântico. QNodes estão vinculados a um dispositivo quântico específico, usado para avaliar valores esperados e de variância deste circuito.

Primeiro, precisamos definir a função quântica que será avaliada no QNode:

def circuit(params):
  qml.RX(params[0], wires=0)
  qml.RY(params[1], wires=0)
  return qml.expval(qml.PauliZ(0))

##############################################################################

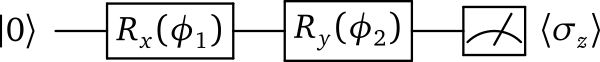
Este é um circuito simples, correspondendo ao descrito acima. Observe que a função ``circuit()`` é construída como se fosse qualquer outra função Python; ela aceita um argumento posicional ``params``, que pode ser uma lista, tupla ou array, e usa os elementos individuais para os parâmetros dos portões. No entanto, funções quânticas são um **subconjunto restrito** das funções Python.

Para que uma função Python também seja uma função quântica válida, existem algumas restrições importantes:

* **Funções quânticas devem conter operações quânticas, uma operação por linha, na ordem em que devem ser aplicadas.**

Além disso, devemos sempre especificar o subsistema ao qual a operação se aplica, passando o argumento ``wires``; este pode ser uma lista ou um inteiro, dependendo de quantos fios a operação atua.

* **Funções quânticas devem retornar um único ou uma tupla de observáveis medidos**.

Como resultado, a função quântica sempre retorna uma quantidade clássica, permitindo que o QNode interfira com outras funções clássicas (e também com outros QNodes).

@qml.qnode(dev1)
def circuit(params):
  qml.RX(params[0], wires=0)
  qml.RY(params[1], wires=0)
  return qml.expval(qml.PauliZ(0))

##############################################################################

Assim, nossa função quântica ``circuit()`` é agora uma: class: pennylane.QNode`.

Que será executado no dispositivo ``dev1`` toda vez que for avaliada.mPara avaliar, simplesmente chamamos a função com algumas entradas numéricas apropriadas:

params = np.array([0.54, 0.12])
print(circuit(params))

Fonte : PennyLane