📊 Como a IA e a Regressão Linear Estão Transformando o Planejamento Industrial
- #Microsoft Copilot
- #Microsoft Copilot Studio
- #Automação
- #.NET C#
- #ChatGPT
- #C #
- #OpenAI Agents
A inteligência artificial está mudando o planejamento estratégico nas indústrias. Um dos impactos mais fortes é na previsão de demanda, permitindo antecipar o crescimento de vendas, ajustar a capacidade produtiva e evitar gargalos na operação.
Neste artigo vou mostrar, passo a passo, como aplicar regressão linear simples (modelagem estatística) para prever vendas futuras — e depois comparar com uma resposta gerada via IA realizando o mesmo cálculo automaticamente.
🔮 Da frase da Compaq à era do Machine Learning
Em 1995, a Compaq declarou:
“O mercado é previsível porque as pessoas são previsíveis.”
Trinta anos depois, esse conceito virou prática: modelos de IA usam machine learning para analisar dados históricos, identificar padrões e prever o futuro com base no comportamento real das pessoas.
🏭 Caso Real: Specific Motors
A Specific Motors (fabricante de motores elétricos) opera quase no limite da capacidade. O gerente de produção quer saber se as vendas continuarão crescendo e se deve expandir as instalações.
📊 Dados históricos de vendas (em milhares de unidades):
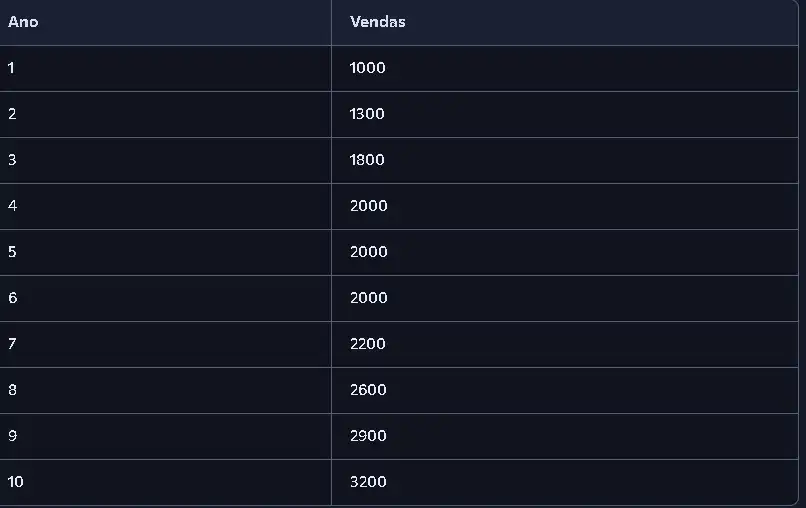
🧮 Regressão Linear Simples
Queremos encontrar a equação: Y=a+bX
Onde:
- x: período (ano)
- y: vendas
- n=10 : número de observações
- x̄ = (55) / 10 = 5.5
- ȳ = (21000) / 10 = 2100
🧮 Fórmulas principais
Médias:
x̄ = (Σx) / n
ȳ = (Σy) / n
Coeficiente angular (inclinação da reta):
b = [Σxy - (Σx * Σy) / n] / [Σx² - (Σx)² / n]
Intercepto da reta:
a = ȳ - b * x̄
Equação da reta de regressão:
y = a + b x
Coeficiente de correlação linear:
r = [Σxy - (Σx * Σy) / n] / sqrt{[Σx² - (Σx)² / n] * [Σy² - (Σy)² / n
Fazendo os cálculos do exemplo anterior da Specific.
Coeficiente angular (b):
b = [soma_xy - (soma_x * soma_y) / n] / [soma_x2 - (soma_x)^2 / n]
b = [133300 - (55 * 21000) / 10] / [385 - (55^2) / 10]
b = [133300 - 115500] / [385 - 3025]
b = 17800 / 82.5 ≈ 215.76
Intercepto (a):
a = media_y - b * media_x
a = 2100 - 215.76 * 5.5 ≈ 913.32
Equação da reta de regressão:
y = 913.32 + 215.76 * x
Previsões:
Ano 11:
y = 913.32 + 215.76 * 11
y = 913.32 + 2373.36
y = 3286.68 ou 3290 milhares de unidades.
Ano 12:
y = 913.32 + 215.76 * 12
y = 913.32 + 2589.12
y = 3502.44
Ano 13:
y = 913.32 + 215.76 * 13
y = 913.32 + 2804.88
y = 3718.20
Esses valores representam a previsão de vendas (em milhares de unidades) para os anos 11, 12 e 13. As previsões são arredondadas para um dígito significativo a mais do que os dados originais. Note que os dados de vendas contém somente dois dígitos significativos; as previsões são arredondadas para três.
📊 Cálculo dos Coeficientes de Correlação (r) e Determinação (R²)
🔹 Coeficiente de Correlação Linear (r)
Este coeficiente mede a força e a direção da relação entre as variáveis x e y. A fórmula é:
r = [Σxy - (Σx * Σy) / n] / sqrt{ [Σx² - (Σx)² / n] * [Σy² - (Σy)² / n] }
🔸 Valores conhecidos:
- Σx = 55
- Σy = 21000
- Σx² = 385
- Σxy = 133300
- n = 10
Agora precisamos calcular Σy². Usando os dados de vendas:

Σy² = 48,180,000
🔹 Substituindo na fórmula:
r = [133300 - (55 * 21000) / 10] /
sqrt{ [385 - (55^2) / 10] * [48180000 - (21000^2) / 10] }
r = [133300 - 115500] /
sqrt{ [385 - 3025] * [48180000 - 44100000] }
r = 17800 / sqrt{82.5 * 4080000}
r = 17800 / sqrt{336600000}
r ≈ 17800 / 18349.73 ≈ 0.97
✅ Coeficiente de Correlação (r) ≈ 0.97
Este coeficiente representa a proporção da variância de y explicada pela regressão:
R² = r² = (0.97)^2 ≈ 0.94
✅ Coeficiente de Determinação (R²) ≈ 0.94
✅ Interpretação
- r ≈ 0.97 → Correlação forte e positiva entre tempo e vendas.
- R² ≈ 0.94 → O modelo explica 94% da variação nas vendas com base no tempo.
Esses valores confirmam que a regressão linear é altamente eficaz para prever a demanda futura da Specific Motors.
📈 Previsões para os Próximos 3 Anos
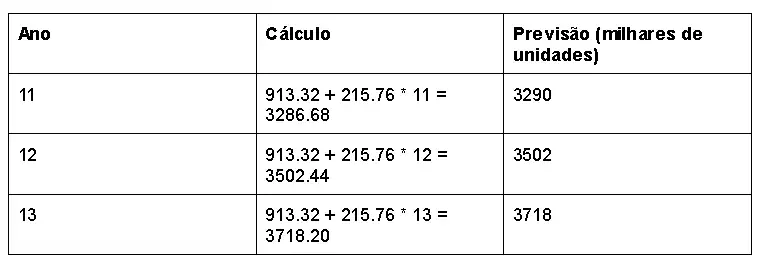
📉 Gráfico (Histórico x Regressão Linear)

🤖 Usando IA para automatizar tudo
Depois de fazer toda a matemática à mão, perguntei à IA:
“Quero previsão de vendas da fábrica Specific Motors para os próximos 3 anos com base nos dados abaixo…”
A IA respondeu com:
- A mesma equação da regressão
- Mesmos coeficientes
- Mesmas previsões
Ou seja:
todo aquele cálculo de páginas e páginas foi resolvido em segundos.
🏭 Impacto no planejamento industrial
Com esse resultado, a Specific Motors pode:
- definir quando ampliar a capacidade produtiva,
- ajustar estoque de matéria-prima,
- planejar investimentos em logística,
- melhorar o fluxo de caixa e compras.
✅ Conclusão
A regressão linear simples mostra que as vendas continuarão crescendo.
A IA realiza o mesmo estudo automaticamente, acelerando decisões estratégicas e reduzindo riscos.
Estatística + IA = planejamento industrial orientado por dados.
Como engenheiro de produção, com ampla experiência em ambiente industrial, eu te convido a testar.
Teste agora — use o prompt abaixo ou crie o seu próprio.
Quero saber se o crescimento de vendas da fábrica prosseguirá, e desenvolver uma previsão a longo prazo a ser usada para planejar as exigências de instalações para os próximos três anos. Os registros de vendas dos últimos dez anos acumularam-se nos dados abeixo. Ano de 1 a 10.
Vendas Anuais (milhares de unidades)
Ano 1 - 1.000
Ano 2 - 1.300
Ano 3 - 1.800
Ano 4 - 2.000
Ano 5 - 2.000
Ano 6 - 2.000
Ano 7 - 2.200
Ano 8 - 2.600
Ano 9 - 2.900
Ano 10 - 3.200
📚 Fonte dos dados do estudo (caso Specific Motors):
GAITHER, Norman; FRAZIER, Greg. Administração da Produção e Operações. 8. ed. São Paulo: Pioneira, 2002.











