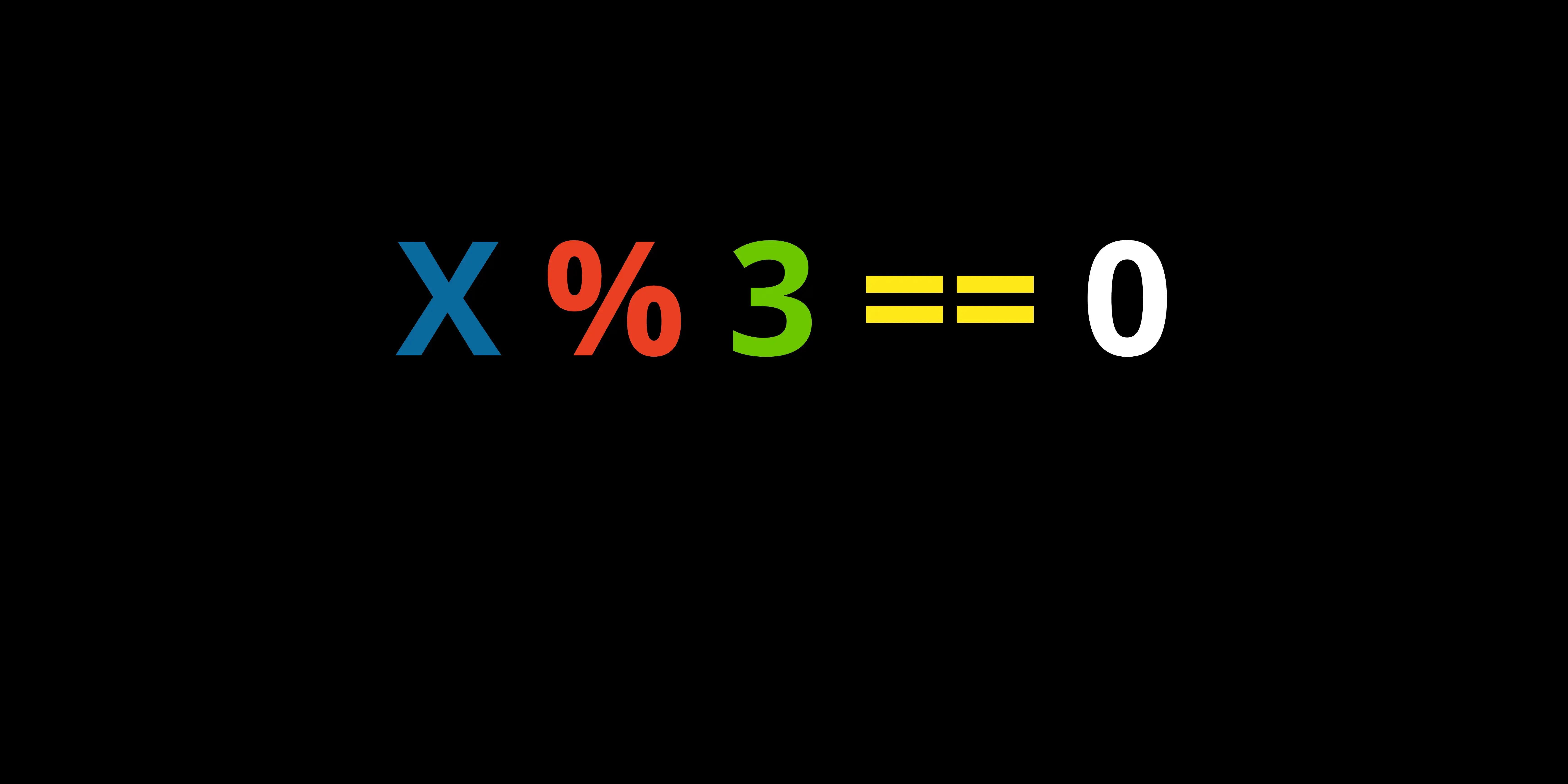PSEUDOCÓDIGO: Como ele pode te ajudar
- #Python
Vai fazer um ano que estudo Python e no começo, os primeiros desafios de código eram muito difíceis pra mim. Sempre pensava, nossa a forma de resolver tal problema o professor tirou do olho, não é possível. Eu sempre tinha dúvidas sobre quais variáveis declarar, se precisava de um contador, de um acumulador, se era caso de if, for, while, range () ... e principalmente se eu tinha conseguido entender a lógica para resolver o problema corretamente. Eu sempre soube que matemática é treino, e que repetição é a ginástica do cérebro. Então, apostei nessas ferramentas pra aprender o que eu precisava e preciso.
Eu tive o prazer de ser alfabetizada em casa, pela minha mãe, e muito do que eu uso hoje para aprender qualquer coisa tem como base tudo que ela me ensinou em 3 anos de educação domiciliar. No estudo da matemática era “fala com os números! Eu quero te ouvir falando com os números”. Sim, ela ficava em outro cômodo enquanto a gente estudava na sala. “Escreve, escreve, porque depois, se tu esquecer se é com x ou ch, a mão lembra”. É claro que com apenas o ensino fundamental, na época, ela não sabia que a memória motora é a memória mais PODEROSA que nós temos. Motivo pela qual não “desaprendemos” a andar de bicicleta.
E o pseudocódigo me lembra muito essa forma de aprender. E foi ele que me salvou para compreender os fundamentos da programação em Python. Se tu pesquisar, existem formas de se expressar no pseudocódigo, eu gosto da mais simples. Aquela me ajuda a entender o problema. Por exemplo:
# Q1: Imprima os primeiros 10 múltiplos de 3.
Além da leitura (e releitura) atenta do problema, podemos ‘falar’ com os números dessa forma:
1.Qual é meu objetivo: encontrar os 10 primeiros múltiplos de 3.
Mas o que é múltiplo de 3? Ora, o múltiplo de 3 é aquele número que ao ser dividido por 3 o resto é igual a zero. Logo, a divisão é exata.
É como em (lendo em voz alta):
6 / 3 = 2, pois 2 x 3 é igual a 6, para 6 não falta nada. Resto zero.
Concluímos que 6 é múltiplo de 3.

Fale com os números e olhe essa imagem. O cérebro humano leva apenas 10 segundos para gravar imagens com detalhes e para memorização a longo prazo é preciso fechar os olhos e refazer a imagem mentalmente.
Em Python fica : x % 3 == 0

Onde se um número x ao ser dividido por 3 tem resto (%) igual (==) zero, então ele é múltiplo de 3.
2.Agora declaramos as variáveis:
Preciso de uma variável para:
Armazenar o limite da repetição, no caso o limite é 10.
Armazenar quantos múltiplos de 3 foram encontrados.
Armazenar o começo da contagem. No caso pode ser x, e o começo da contagem deve ser em 0 (ou outro valor que tu decidir).
Então teremos:
Quantidade = 10 # limite da repetição
Contagem = 0 # A contagem começa em zero
x = 0 # Os números começam em zero
3. Penso na estrutura do loop:
Como eu disse anteriormente, quanto mais tu treinar resolver questões, mais fácil será de pensar em estruturas para resolver problemas. A repetição ajuda a formar um ‘padrão’ de solução de problemas que é acionado ao encontrar problemas semelhantes.
Para saber quais são os números que são múltiplos de 3, vamos ter que percorrer a sequência de números até 10, certo?
O loop vai verificar cada número x,
Se x for múltiplo de 3 ele imprime e incrementa em ‘contagem’
O loop vai continuar até alcançar ‘quantidade’ (definida anteriormente como 10).
x vai precisar aumentar a cada iteração para passar pro próximo número.
O raciocínio sobre a estrutura de loop, o uso de acumuladores, somadores ou a própria lógica do algoritmo virá naturalmente conforme tu ganha experiência em resolver problemas.
5.Pseudocódigo:
Definir quantidade como 10
Inicializar a contagem como 0
Inicializar x como 0
Enquanto contagem for menor que quantidade:
Se x for múltiplo de 3:
Imprimir x
Incrementar contagem
Incrementar x
O pseudocódigo foca na LÓGICA do problema e não na sintaxe. Quanto mais tu ler, quanto mais tu “falar” com os números, quanto mais tu “escrever”, maiores as chances do teu cérebro armazenar o padrão de resolução de problemas. Treine e resolva questões para ganhar experiência.
TESTE DE MESA
Algo que gosto de fazer é o teste de mesa. O teste de mesa para compreender problemas simples (e armazenar padrão para resolver problemas complexos) também é como “falar em voz alta com os números”.
Por exemplo:

‘fim’ armazena o limite da repetição. Até que número vai a contagem.
Uma variável ‘a’ armazena 0.
Uma variável ‘b’ armazena 1.
Numa sequência de números, ‘a’ será igual a b, e ‘b’ será igual ao resultado de
‘a + b’.
Assim, ‘a’ será sempre atualizado até o limite de…digamos 13 números na sequência (se o input for 13).
Quando ‘a’ for 0 e ‘b’ for 1, que é o começo da sequência, os números seguintes serão:
‘a’ atualizado com o valor de ‘b’, enquanto ‘b’ é o valor de ‘a + b’.
Exemplo:

Ao imprimirmos a sequência, os próximos números (que começou em 0,1) serão a soma dos 2 anteriores.
Imprimimos ‘a’ pois ele é quem é atualizado com o valor de b (a+b).
Declarando: # Tópico sobre atribuição de múltiplas variáveis em python ou tupla.
a, b = 0, 1
a, b = b, a + b
fim = # limite da repetição
Lendo em voz alta as iterações:

Primeira iteração: ‘a’ é 0, ‘b’ é 1 como declarado.
Segunda iteração: ‘a’ é 1 (a=b), b é 1 (a + b ou 0 + 1 =1).
Terceira iteração: ‘a’ é 1 (a=b), ‘b’ é 2 (a + b).
Quarta iteração: ‘a’ é 2 (a=b) , ‘b’ é 3 (a + b).
Quinta iteração: ‘a’ é 3 (a=b) , ‘b’ é 5 (a + b).
Sexta iteração: ‘a’ é 5, ‘b’ é 8 (a + b).
Sétima iteração: ‘a’ é 8, ‘b’ é 13.
Nas próximas ‘a’ será ‘13’ e ‘b’ será 21, e assim por diante.
Essa sequência de números é conhecida como Sequência de Fibonacci.
Você pode ler e preencher os ‘quadradinhos’ a cima manualmente enquanto lê a lógica. Conforme for lendo a lógica, ela será armazenada na sua memória de trabalho. E cada vez que tu precisar resolver uma iteração tu poderá ‘ver’ a lógica modelada e ela poderá ser acessada para resolver problemas semelhantes.
Em certas condições (nível de atenção, de concentração ), o cérebro pode levar até 10 segundos para memorizar uma imagem mais detalhada. Se tu é iniciante, assim como eu, precisa ganhar experiência em resolver questões e precisa ‘falar’ com as estruturas. Treine resolver questões mentalmente e gaste o tempo necessário até ficar bom nisso. Com a experiência formamos "modelos" mentais que são acionados automaticamente ao encontrar problemas semelhantes. Com o tempo, o teu cérebro começa a reconhecer rapidamente padrões em problemas e sabe quais ferramentas ou abordagens utilizar, sem precisar pensar muito sobre cada detalhe. Esse conceito está relacionado à memória procedural.
Algo me ajuda muito, no caso de python, é resolver todos os exercícios do livro de estudo. Para cada tópico peço ao ChatGPT para fazer questões das mais simples às mais complexas para ganhar experiência em aprender a pensar em resolução de questões. Também gosto de resolver questões de acompanham cursos de programação da USP, os pdf das aulas são fáceis de encontrar.
Portanto, quanto mais tu pratica, mais rápido é capaz de identificar padrões e aplicar soluções de forma quase automática!
Livros:
Introdução a programação com python, Nilo Ney Coutinho.
Pense em Python, Allen B. Downey.
Exemplo de PDFs-USP
Boa semana e bons estudos a todos.